개발이글스
[자료구조] Data Structures, Algorithms and Time Complexity 본문
[자료구조] Data Structures, Algorithms and Time Complexity
지윤이글스 2023. 1. 11. 14:43자료구조와 알고리즘을 공부하기에 앞서 자료구조와 알고리즘이 무엇인지, 둘의 차이는 무엇인지 알아보자
1. 자료구조(Data Structure)
먼저, 자료구조는 말 그대로 자료(data)를 담는 구조이다. 여러 데이터들의 묶음을 저장하고 사용하는 방법을 정의한 것이다. 데이터를 효율적으로 다룰 수 있는 여러 방법들을 모아 "자료구조" 라고 한다.
자료구조는 특정한 상황에 놓인 문제를 해결하는데 특화 되어있다. 많은 자료구조를 알아두면 알고리즘테스트와 같은 상황에서 적합한 자료구조를 이용해서 빠르게 문제해결이 가능해진다.
==> 가장많이 쓰이는 자료구조 : Stack, Queue, Tree, Graph -> (스택, 큐, 트리, 그래프)
2. 알고리즘 (Algorithm)
어떤 문제를 해결하기 위해 사용되는 풀이과정을 말한다. 즉, "문제 해결 방법" 이다.
수학에서 한 문제에 대해 여러가지 풀이법이 존재하는 것처럼, 프로그래밍 또한 한 문제에 대해 여러 풀이법이 존재한다.
여러가지 풀이법 중 가장 효율이 좋은 방법을 어떤문제에 대한 알고리즘 이라고한다.
수학의 공식처럼, 특정 형태 또는 구조를 갖는 프로그래밍 문제에는 공식화된 알고리즘이 존재한다.
==> 알고리즘 종류 : Sort(정렬) , Search(탐색), Graph(그래프)
알고리즘 문제를 풀다보면 문제에 대한 해답을 찾는것이 가장 중요하다. 그러나 그에 못지않게, 효율적인 방법으로 문제를 해결했는지도 중요하다. 혹시 문제를 풀다가 이것보다 더 효율적인 방법은 없나? 하고 고민해봤다면 시간복잡도를 고민한다는 것과 같은 말이다. 시간복잡도와 Big-O(빅-오)표기법을 알아보자.
3.시간복잡도(Time Complexity)
알고리즘의 스피드는 "완료까지 걸리는 절차의 수" 로 결정된다. 따라서 같은 작업을 수행하는데
딱 5번의 단계로 수행되는 알고리즘이 10개의 단계가 필요한 알고리즘보다 훌륭한 알고리즘이겠죠?
알고리즘의 로직을 코드로 구현할 때, 시간 복잡도를 고려한다는 것은 "입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?" 라는 말이다.
효율적인 알고리즘을 구현한다는 것은 바꾸어 말해 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 이야기 이다.
그리고 이 시간복잡도는 주로 빅-오 표기법을 사용해서 나타낸다.
▶ Big-O 표기법 : 시간복잡도를 표기하는 방법
- Big-O(빅-오) -> 상한 점근
- Big-Ω(빅 오메가) -> 하한 점근
- Big-θ(빅-세타) ⇒ 그 둘의 평균
위 세가지 표기법은 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법이다.
※가장 자주 사용되는 표기법 - 빅오 표기법
빅오 표기법은 최악의 경우를 고려하므로, 프로그램에서 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있기 때문이다.
※시간복잡도 최선의 경우를 고려한경우
: 최선의경우 1초, 최악의경우 1시간이 걸리는 알고리즘을 구현했고, 최선의 경우를 고려한다고 가정해보자. 이 알고리즘을 100번 실행한다면 최선의 경우 100초가 걸린다. 만약 실제로 걸린시간이 1시간을 훌쩍 넘겼다면, "어디에서 문제가 발생한거지?" 라는 의문이 생긴다. 최선의경우만 고려했으니, 어디에서 문제가 발생했는지 알아내기 위해서는 로직의 많은 부분을 파악해야 하므로 문제를 파악하는데 많은 시간이 필요하다.
※시간복잡도의 최악의 경우를 고려한 경우
최악의 경우가 생기지 않기를 바라며, 시간을 계산하는것보다 "최악의 경우도 고려하여 대비" 하는것이 바람직하다.
따라서 빅오 표기법이 가장 많이 사용된다. 빅오 표기법은 "입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?" 를 표기하는 방법이다.
※빅오 표기법의 종류
- O(1)
- O(n)
- O(log n)
- O(n2)
- O(2n)
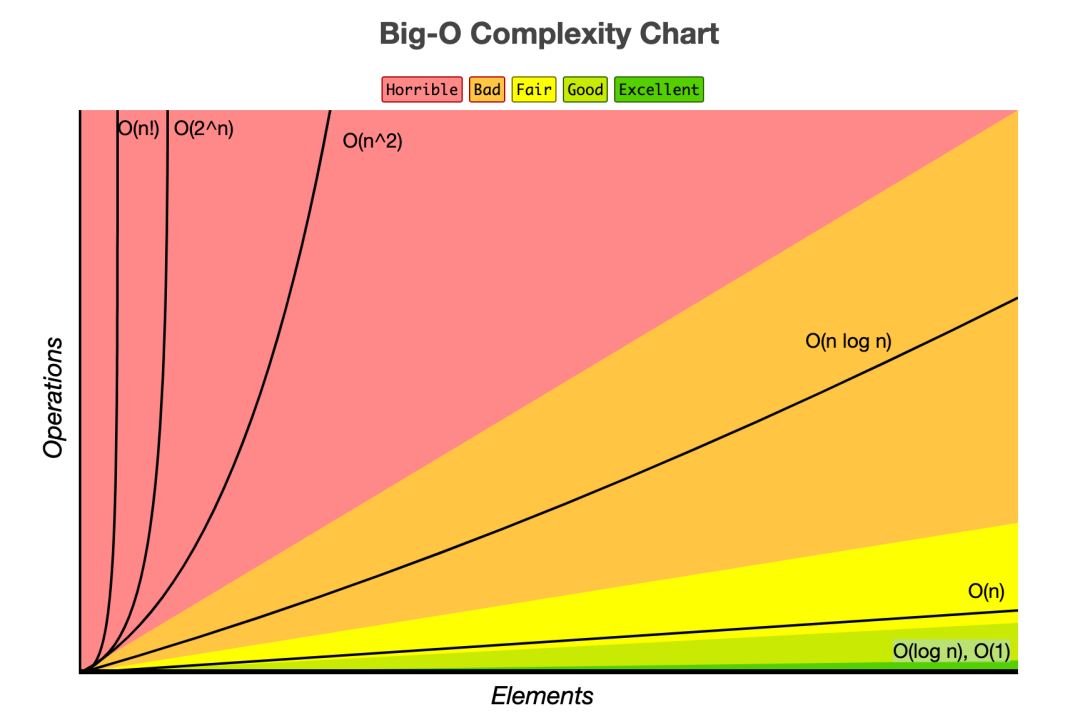
1. O(1) 는 일정한 복잡도 ( constant complexity) 라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다. 다시말해 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미이다.
2. O(n) 은 선형 복잡도(linear complexity) 라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다. 예를 들어 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때, 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n) 의 시간 복잡도를 가진다는 의미이다.
3. O(log n) 은 로그복잡도(logarithmic complexity) 라고 부르며, 빅오 표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
4. O(n2)은 2차복잡도(quadratic complexity) 라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는것을 의미한다. 예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면 이 알고리즘의 시간복잡도는 O(n2) 라고 표현한다.
#참고사이트
'Computer Science > Data Structures' 카테고리의 다른 글
| [자료구조] 그래프 (0) | 2023.01.16 |
|---|---|
| [자료구조] Depth First Search, DFS (깊이 우선 탐색) (0) | 2023.01.14 |
| [자료구조] Tree & Binary Search Tree (0) | 2023.01.14 |
| [자료구조] 스택(Stack) & 큐(Queue) (0) | 2023.01.12 |
| [자료구조] 배열(Array) & 리스트(List) +ArrayList (0) | 2023.01.11 |



